Two types of DAS system
- Intensity-based system
- first gen
- not quantitive
- cheaper & robustness
- Amplitude of Rayleigh backscattered energy
- Phase-based system
- second gen
- quantitative
- expansive
Intensity based system
Principle of intensity-based system
The perturbed fiber will have a different intensity image:
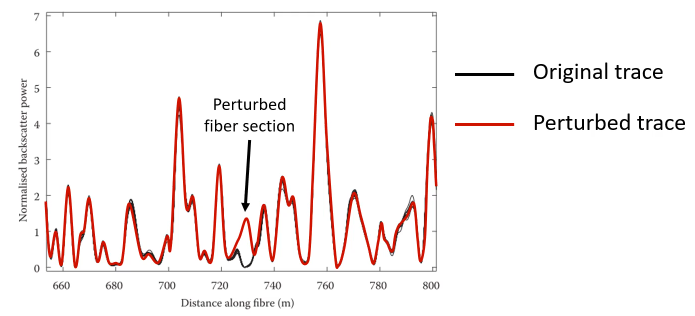
Experiments on intensity-based system
2-m fiber -> non-linear and random. Not easy to use.
Phase based system
Complicated, but could provide quantitative result.
Principle
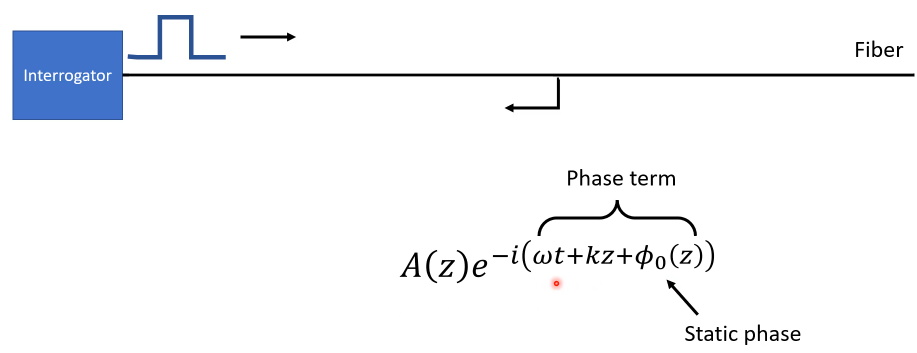 The first pulse: \(\delta\phi_1(z,t_1)=\phi(z+\delta z, t_1)-\phi(z,t_1)=2k\Delta z+c_0\)
The first pulse: \(\delta\phi_1(z,t_1)=\phi(z+\delta z, t_1)-\phi(z,t_1)=2k\Delta z+c_0\)
The second pluse: because of the strain in fiber, there will be a distortion \(\delta z\).
\[\delta\phi_2(z,t_1)=\phi(z+\delta z, t_2)-\phi(z,t_2)=2k\Delta z+2k\delta z+c_0\]The differential phase: \(d\phi(z, t_1) = \delta \phi_2-\delta \phi_1=2k\delta z\)
Note that \(\delta z\) is much smaller than \(\Delta z\). Change in length will change in refractive index(assume it’s linear).
Then, \(\delta \phi = \frac{4\pi nL_G}{\lambda}[\frac{\Delta x}{x}+\frac{\Delta n }{n}]\)
–> \(\delta \varepsilon_{xx}(t, x_j)\approx 1.16\times 10^{-10}\delta \Phi(rad)\)
Note that this is happened in one time and one channel.
文档信息
- 本文作者:Shenyao Jin
- 本文链接:https://shenyaojin.github.io/2022/07/12/DAS-intro/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)