Introduction to seismic wave

P wave and S wave.

DAS as a strain rate sensor
- seismic wave length is much larger than gauge length
- gauge length effect can be ignored

Receiver frequency responses

Velocity Spectrum: \(\dot u=A(\omega)e^{i(\omega t-kx)}\) Acceleration Spectrum: \(\ddot{u}=-i\omega\dot u\)

We know particle velocity: \(\dot u(z,t)=V_P(z, t) = Ae^{i(\omega t-kz)}\)

Strain: \(\dot\varepsilon(z,t) = \frac{d\dot u}{dz}=-A\cdot ik\cdot e^{i(\omega t-kz)}\)

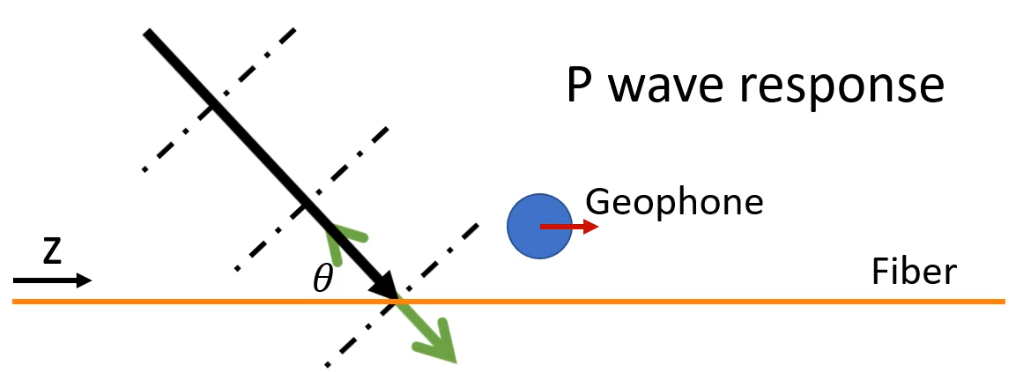
There will ba an angle in most situation:

Geophone:

\[\dot\varepsilon(z,t) = \frac{d\dot u}{dz}=-\vec A\cdot\hat{\vec z} ik\cdot e^{i(\omega t-kx)}=A\sin\theta e^{i(\omega t-kx)}\]

DAS: \(\dot\varepsilon(z,t) = \frac{d\dot u}{dz}=-\frac{1}{2}iAk\cdot\sin 2\theta\cdot e^{i(\omega t-kx)}\)

Note that \(\hat z\) is const while getting the derivative.

\[\mathrm{DAS\ Channel\approx Geophone2(t)-Geophone1(t)}\]

\(\mathrm{DAS(t)}=A(-1+e^{ikL_G})e^{i(-\omega t+\Phi_0)}\)

DAS amplitude: \(A_{DAS}^2=2A^2(1-\cos(kL_G))\)

while \(k=\frac{2\pi}\lambda\).

Thus if \(L_G=\lambda, A_{DAS}=0\).

\(L_G\): Gauge length; k is wave number.

\[A_{DAS}^2=2A^2(1-\cos(k_{app}L_G))\]

while \(k_{app}=\frac{2\pi}{\lambda_{app}}\). And

\[\lambda_{app}=\frac{\lambda}{\cos\theta}\]

If \(kL_G\ll1\), we have:

\[\cos(kL_G)\approx1-\frac{k^2L_G^2}{2}\]

Then,

\[A_{DAS}=AkL_G\]

So it’s still linear.