Introduction

DTS(Distributed Temperature Sensing) focuses on Raman backscatters, compared to DAS, which focused on Rayleigh backscatters.

Raman scattering

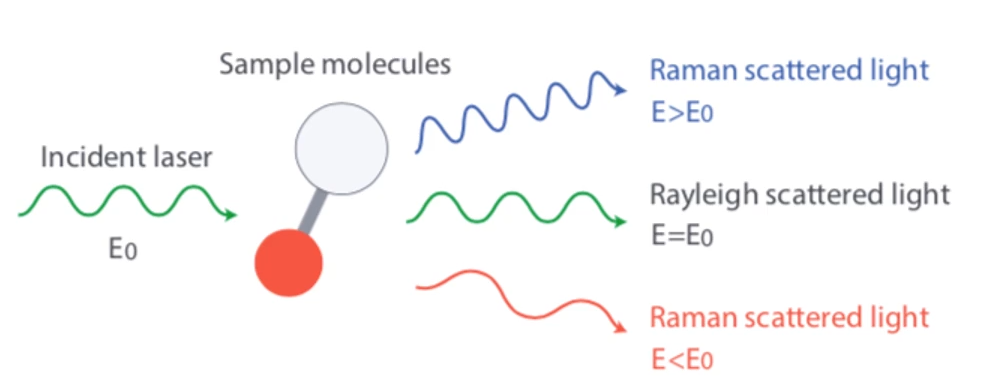
• Raman scattering <-> Molecular vibration <-> Temperature
• Note that the T must be in Kelvin.

It could be simplified to the following formula, applying the ratio:

It’s obvious that the low temperature is less sensitive than high temperature from the formula.

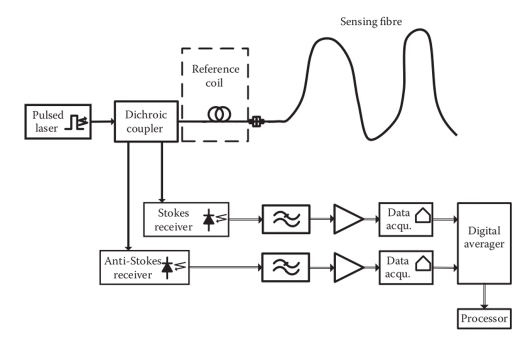
Propagation in fiber

It has a different co-efficient in that OTDS formula from DAS:

\(P_{as}(z) = E_p(0)\cdot \eta_{as}(z)\cdot exp(-\int_{0}^z(\alpha_p(u)+\alpha_{as}(u))\cdot du)\)

• In most cases we only measure the amplitude ratio, for it will erase most of the terms.

With a propagation x = z: \(R(T(z)) = (\frac{K_{as}}{K_s})(\frac{\lambda_s}{\lambda_{as}})^4exp(-\frac{S_{LE}}{T})\cdot exp(-\int_{0}^z(\alpha_p(u)-\alpha_{as}(u))\cdot du\)