Why Calibration?

There’s attenuation factors, they are different from fiber to fibers, and varies from time/space.

If the correction factor we applied is not accurate, this could add a spacial volume bias to the temperature measurement.

Where’s attenuation?

There’s time-dependent offset and differential attenuation(spatial variable)

Temperature offset

It’s time-dependent, so: \(\frac{1}{T_c(z, t)} = \frac{1}{T_0(z,t)}+c(t)\)

Differential attenuation

It’s spatially dependent: \(\frac{1}{T_c(z,t)}=\frac{1}{T_0(z,t)}+\alpha_Cz\) t should be in Kelvin.

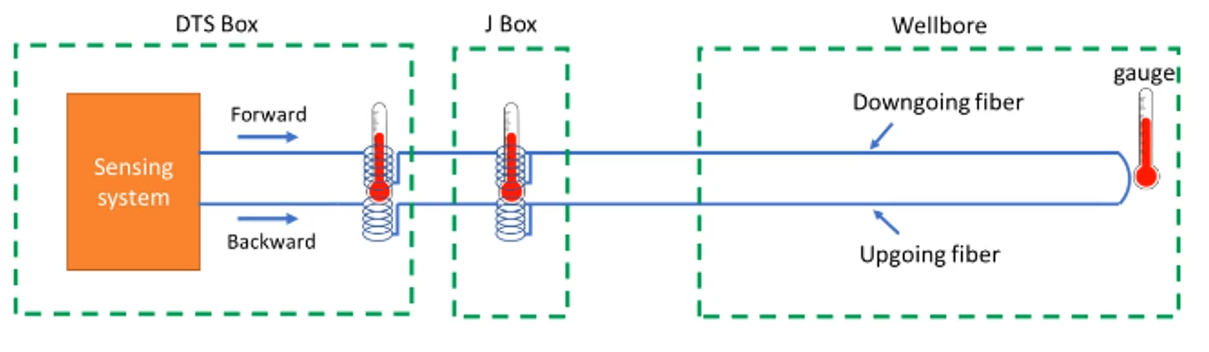
Calibration: single-ended setup

Reference temperature box thermal controlled box with a coil of fiber connected to sensing fiber.

Two step calibration

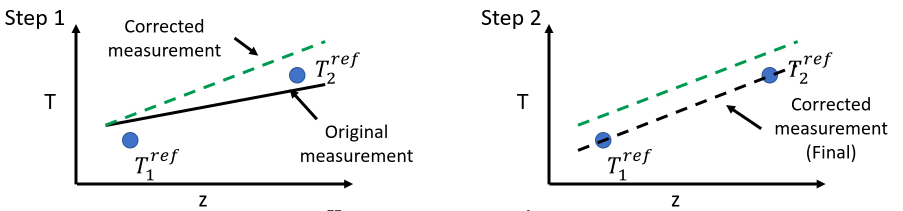
1. find a constant \(\alpha_c\) that the difference at two boxes are corrected.
2. find a c(t) that the temperature measurements at reference boxed are consistent.

Shortcoming: not so accurate while the temperature variation is big. Also, the attenuation is related to strain as well.

Calibration: double-ended setup

It’s a widely used processing method in seismology. \(R_{E1}(T(z))=\frac{K_{as}}{K_S}(\frac{\lambda_s}{\lambda_{as}})^4exp(-\frac{S_{LE}}{T(z)})\cdot exp(-\int_0^z(\alpha_{as}(u)-\alpha_{s}(u))\cdot du)\)

Calculating: \(\sqrt{R_{E1}(T(z))R_{E2}(T(z))}\) , there will not be mistakes.