Attenuation and Skin Depth

Attenuation

Attenuation defines the rate of amplitude loss an EM wave experiences at it propagates. The attenuation of an EM wave is defined by the parameter \(\beta\). For a down-going planewave, the attenuation is defined as: \(A(z) = A_0e^{\beta z}\) where \(A\) is the amplitude while \(A_0\) is the absolute amplitude at \(z=0\)m and:

\(\beta=\omega(\frac{\mu\epsilon}{2}[(1+\frac{\sigma^2}{\epsilon^2\omega^2})^{\frac12}-1])^{\frac12}\ge0\)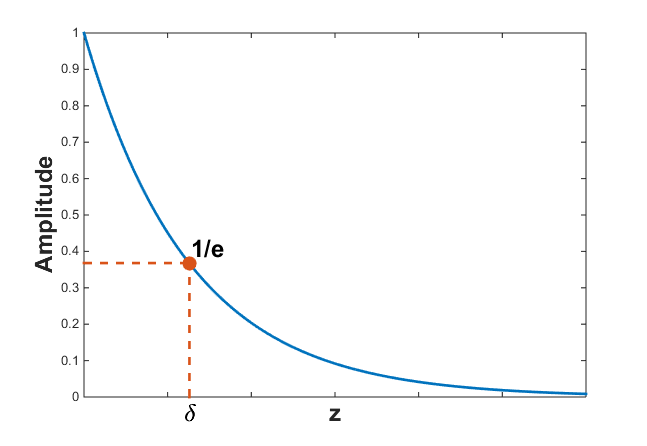

Skin Depth

Skin depth defines the distance that a wave must travel before its amplitude has decayed by a factor of 1/e. The skin depth is the reciprocal of the decay constant \(\beta\).

Since \(\beta\) depends on the frequency and the physical properties of the media, so does the skin depth. For a general case, the skin depth can be considered a fairly complicated function. However, approximations exist in the quasi-static and wave regimes.

Approximations

In the wave regime(\(\epsilon\omega\gg \sigma\)), the skin depth is approximately equal to: \(\delta=\frac1\beta=\frac2\sigma\sqrt{\frac{\epsilon}{\mu}}\)